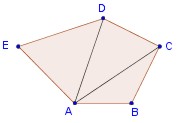
Un polígono está formado por elementos básicos. Éstos son:
1. vértice
2. lado
3. ángulo interior
4. ángulo exterior
5. diagonal
1. Vértice: es el punto de intersección de dos segmentos contiguos. Se designan con una letra mayúscula A, B, C, D...
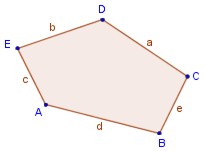
2. Lados: es cada uno de los segmentos de recta que forman el polígono. Se designa con dos letras mayúsculas ubicadas en sus extremos, o con una letra minúscula en correspondencia con el vértice opuesto: AB = d, BC = e , CD = a, DE = b, EA = c
3. Ángulo interior: es el ángulo formado por dos lados del polígono. El ángulo interior se designa con una letra griega o con las tres letras mayúsculas de los vértices que correspondan.
4. Angulo exterior: es el ángulo formado por un lado y la prolongación de otro contiguo hacia la región exterior. Generalmente se designa con la letra griega del ángulo interior adyacente acompañada de un subíndice
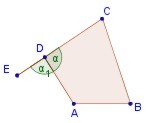
5. Diagonal: es el trazo que une dos vértices no consecutivos del polígono. Se designa con las dos letras mayúsculas correspondientes a los vértices que se unen, o por una letra d con subíndice: AC =d1, AD = d2.
Apotema de un polígono regular
La apotema de un polígono regular es el segmento perpendicular a un lado desde el centro del polígono. Es básica para conocer el área del polígono ya que es la altura de cada uno de los triángulos formados por cada dos radios y el lado.
Elementos secundarios de un polígono
En todo polígono (el triángulo es un polígono) podemos obtener elementos secundarios como:
Bisectrices, se denomina bisectriz al rayo que dimidia al ángulo, es decir, lo divide en 2 partes iguales.
Simetrales, la simetral es una recta perpendicular que dimidia a un trazo.
Alturas, una altura, cuyo símbolo es h, es el trazo perpendicular que une un lado del triángulo con el vértice opuesto.
Transversales, la transversal es el segmento que une el punto medio de un lado con el vértice opuesto.
Medianas, son los segmentos que unen los puntos medios del triángulo.

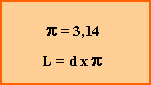
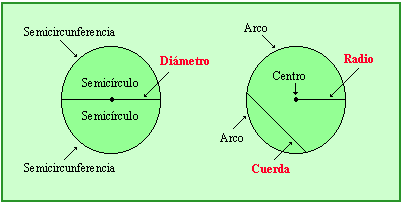
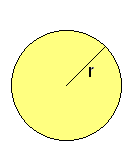
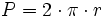
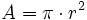
 : número Pi = 3,14159...
: número Pi = 3,14159...